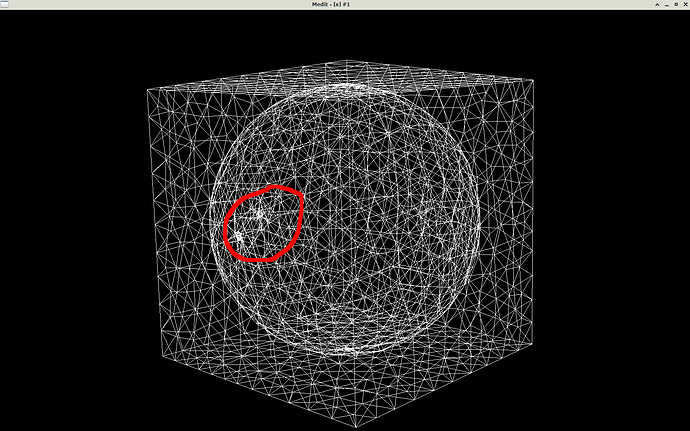
Thanks, @Algiane . Yep, I’m fine. Without I/O it is much more usable now and the sphere mesh generated by the program now looks good! Ok, I see what angle detection does. It seems I can’t turn it off because the edges of the input cube are necessary. So, is the following program what you recommend to do at the end? I rewrote your program but turned angle detection on, and removed I/O, instead just memorizing vertices and tetrahedra in a buffer between iterations.
#include <mmg/mmg3d/libmmg3d.h>
#include <math.h>
#include <stdio.h>
#include <stdlib.h> // for malloc
int main() {
MMG5_pMesh mmg3dMesh = NULL;
MMG5_pSol mmg3dSol = NULL;
MMG3D_Init_mesh(MMG5_ARG_start, MMG5_ARG_ppMesh, &mmg3dMesh, MMG5_ARG_ppMet, &mmg3dSol, MMG5_ARG_end);
MMG3D_Set_meshSize(mmg3dMesh, 8, 6, 0, 0, 0, 0);
// the corners of the unit cube
MMG3D_Set_vertices(mmg3dMesh, (double[]) { 0, 0, 0, 1, 0, 0, 1, 1, 0, 0, 1, 0, 0, 0, 1, 1, 0, 1, 1, 1, 1, 0, 1, 1 }, NULL);
// a tet mesh of the unit cube
MMG3D_Set_tetrahedra(mmg3dMesh, (int[]) { 3, 6, 7, 8, 2, 5, 6, 8, 1, 2, 4, 5, 2, 4, 5, 8, 2, 3, 6, 8, 2, 3, 4, 8 }, NULL);
// refine this tet mesh to have max edge length 0.5 to split all edges
MMG3D_Set_dparameter(mmg3dMesh, mmg3dSol, MMG3D_DPARAM_hmax, 0.5);
MMG3D_mmg3dlib(mmg3dMesh, mmg3dSol);
// let's now run an iterative procedure ten times to refine the mesh
for (int j = 0; j < 10; j++) {
int np, ne;
MMG3D_Get_meshSize(mmg3dMesh, &np, &ne, NULL, NULL, NULL, NULL);
double* verts = malloc(3 * np * sizeof(double));
int* elements = malloc(4 * ne * sizeof(int));
MMG3D_Get_vertices(mmg3dMesh, verts, NULL, NULL, NULL);
MMG3D_Get_tetrahedra(mmg3dMesh, elements, NULL, NULL);
// Free mesh and reopen it to have a clean analysis
// As we want to discretize a new isovalue, cleans all info related to previous isovalue:
// - interior and exterior domains;
// - triangles on the isosurface;
// - ridge and non-manifold tags added to edges at interface of the bounding box and previous isosurface.
// by freeing everything and reading the vertices back in.
MMG3D_Free_all(MMG5_ARG_start, MMG5_ARG_ppMesh, &mmg3dMesh, MMG5_ARG_ppMet, &mmg3dSol, MMG5_ARG_end);
MMG3D_Init_mesh(MMG5_ARG_start, MMG5_ARG_ppMesh, &mmg3dMesh, MMG5_ARG_ppMet, &mmg3dSol, MMG5_ARG_end);
MMG3D_Set_meshSize(mmg3dMesh, np, ne, 0, 0, 0, 0);
MMG3D_Set_vertices(mmg3dMesh, verts, NULL);
MMG3D_Set_tetrahedra(mmg3dMesh, elements, NULL);
MMG3D_Set_solSize(mmg3dMesh, mmg3dSol, MMG5_Vertex, np, MMG5_Scalar);
for (int i = 1; i < np + 1; i++) {
double x, y, z;
MMG3D_Get_vertex(mmg3dMesh, &x, &y, &z, NULL, NULL, NULL);
// signed distance to the unit sphere inside the cube
MMG3D_Set_scalarSol(mmg3dSol, sqrt(pow(x - 0.5, 2) + pow(y - 0.5, 2) + pow(z - 0.5, 2)) - 0.5, i);
}
// Specify to Mmg that we want to discretize a new isovalue
MMG3D_Set_iparameter(mmg3dMesh, mmg3dSol, MMG3D_IPARAM_iso, 1);
MMG3D_Set_iparameter(mmg3dMesh, mmg3dSol, MMG3D_IPARAM_verbose, 5);
// turn angle detection on
MMG3D_Set_iparameter(mmg3dMesh, mmg3dSol, MMG3D_IPARAM_angle, 1);
MMG3D_Set_dparameter(mmg3dMesh, mmg3dSol, MMG3D_DPARAM_ls, 0);
MMG3D_Set_dparameter(mmg3dMesh, mmg3dSol, MMG3D_DPARAM_hmin, 0.05);
MMG3D_Set_dparameter(mmg3dMesh, mmg3dSol, MMG3D_DPARAM_hmax, 0.1);
MMG3D_mmg3dls(mmg3dMesh, mmg3dSol, NULL);
free(verts);
free(elements);
}
MMG3D_saveMesh(mmg3dMesh, "x.meshb");
MMG3D_Free_all(MMG5_ARG_start, MMG5_ARG_ppMesh, &mmg3dMesh, MMG5_ARG_ppMet, &mmg3dSol, MMG5_ARG_end);
return 0;
}
We might be nearing the solution to the old problem Can mmg3d be used to turn an unconstrained to a constrained Delaunay tetrahedralization? .
However, I really wonder why what we’re doing is so complicated. It’s all about having mmg respect boundaries between materials … say, plastic and steel for a heat conduction problem. Respecting material boundaries should be a very common task in tetrahedral meshing. That was and is the motivation for all my questions.
Cheers, Mathias
(By the way, I’m not using cmake but instead I link dynamically and specify the location of include folder, and mmg.lib and mmg.dll explicitly in Visual Studio because my main project simply doesn’t use cmake. Recently, I had to include not only the folder
[installation directory]\include;
but also the folder
[installation directory]\include\mmg;
It seems this is not quite the intended behaviour, is it? All of this is a little complicated because the mmg source files include files that do not exist in the source tree, only in cmake’s copy of it inside the build directory.)
 ?
?

 ), the algorithm to generate the interior mesh of an input triangulation is the following:
), the algorithm to generate the interior mesh of an input triangulation is the following: