Dear mmg developers,
I’m very interested in using mmg for topology optimisation, particularly, inverse homogenisation using mesh evolution.
I’ve noted from the other forum posts that periodic meshing has not been implemented when the level set function intersects the bounding box. I wonder if there is any simple ways around this? Is the discussion here possible in 3D? If so, could I get a few more details (as I’m new to mmg)?
Thanks a lot,
Zachary
Hello,
In general, I think that the method explained applies to 3D. However, it is technically a little harder to implement and this will require you to tweak the numbering of your mesh: in 3D, for some configurations of element splitting, the splitting of the faces is not unique.
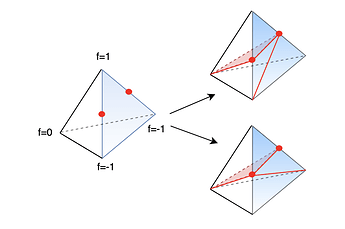
You can look for example at the attached picture : left, you have your input tetrahedra whose level-set values at nodes are given by the f=<x> texts. The blue face is a periodic boundary face. Provided the level-set values we have to split 2 edges to create the isosurface associated to the 0-levelset. The nodes that we have to insert are marked by red points).
There are 2 splittings of the tetrahedra, depicted on the right of the figure, that allow to split the wanted edges and to create the wanted surface (red surface). Both splits create different cuts of the boundary face.
To choose the cutting to be performed Mmg uses magnitude comparisons between the global indices of the vertices of the tetra. Thus, if you take care to have a suitable numbering of your periodic surfaces (the vertices order has to be the same on both sides), I think that you can obtain a consistent result.
Maybe @Yuki will have some feedback on the process (I may have underestimated some of the difficulties).
Best Regards,
Algiane
Thank you for the details @Algiane. I’ll look into this solution in the coming weeks and update this post.
Cheers,
Zachary
Hi @GiacomoSperoni97,
I ended up going down a different route. I would still be interested in solving it though.
