Mmg3d adaptation & mshmet

[mrbenson75]

Hello,

I’d like to perform mesh 3d refinement using a metric sol file but i don’t know how to generate it. There’s a link to mshmet but the mshmet1_3d.c is empty.
At this moment i only have the temperature scalar field and the vector flux field of the solution on the original mesh. How to compute the metric field ?

Thanks for helping.

[Algiane]

Hi,

You can load the olderVersionThatWorks branch of mshmet to have the 3D implementation of the metric computation.

Then, if you run mshmet -h, you will see the list of available options. For most of cases, you will have to set the -eps parameter (tolerence over the error of P1 interpolation), and the -hmin and -hmax values (resp. minimal and maximal edge lengths).
By default, mshmet computes an anisotropic tensor, the -iso argument allows to switch in isotropic mode.

I hope that it will help you.

Best Regards,
Algiane

[mrbenson75]

1 - I compiled mshmet but i get “segmentation fault”… I just modified the source code hessls.c as follow

static int gauss(int n,double** m,double *x,double *b,char dbg)

2 - I just realized that mmg3d allow to set an input solution file as option but it seems to do nothing execpt coarsing the initial mesh. It would be very grateful if you could take a look at the attached example files. I just use mmg3d as follow :

mmg3d -sol temp.sol temp.mesh

Best regards.

temp.mesh (727.9 KB)
temp.sol (89.0 KB)

[Algiane]

Hi,

1.

To use mshmet on your mesh + solution couple, you can run the following command :

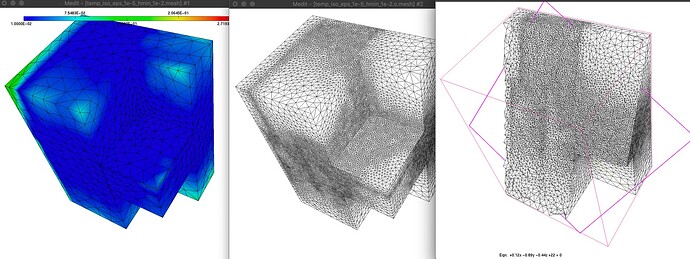
mshmet temp.mesh  -eps 0.00001 -hmin 0.01 -iso

It creates a temp.new.sol file that contains the computed metric. To find suitable values for the parameters, I find more easier to always start in iso mode (even if I finally want an anisotropic metric). Normally it is not too hard to set the hmin value (you just have to know the size for which you will consider your edges too small). Then I just play with the eps parameter until obtaining a satisfying result.
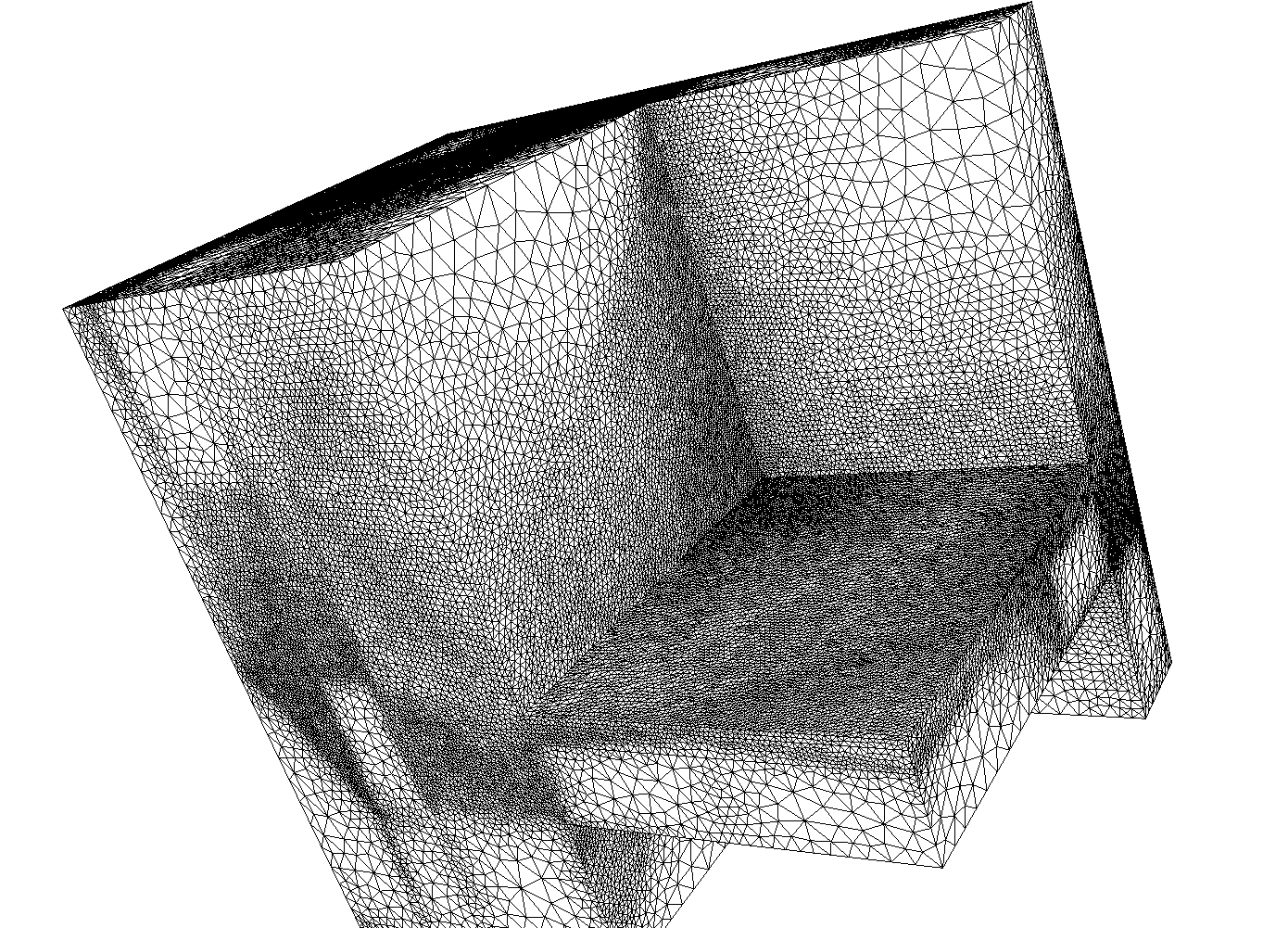
With these parameters, I obtain the metric shown (left) and after adaptation, the two meshes in the middle and on the right. In the middle we see the surface mesh, on the right a volume section.

For the adaptation step, I have used the develop branch of Mmg (because this branch contains some fixes for anisotropic meshes) and I have run the following command :

mmg3d_O3 temp.mesh -sol temp.new.sol

To obtain an anisotropic metric, you can run mshmet with the same parameters but without the -iso argument. Then, for Mmg, as mshmet impose its own gradation, I recommand to disable entirely all the Mmg gradations (besides I have to correct bugs in the required gradation (-hgradreq parameter)):

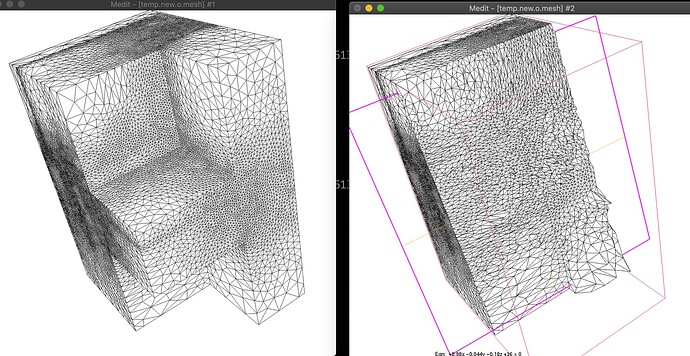
mmg3d_O3 temp.mesh -sol temp.new.sol  -hgrad -1 -hgradreq -1 -nosizreq

I obtain the following results after adaptation (left you have the surface adaptation, right a cut through the volume):

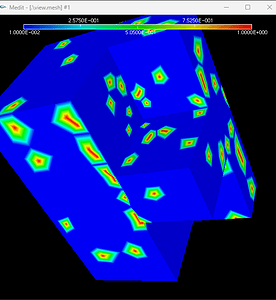
It is not very aniso but the test case is difficult : you have lot of singularities (corners, non-manifold edges and sharp angles) in your mesh and such entities propagates isotropic ratio and in addition the input mesh is coarse so there are not lot of internal nodes to reach higher anisotropic ratio while keeping good qualities elements. I think that aniso ration will increase after few steps of adaptation…

2.

In fact you can’t pass directly your solution field to Mmg (you can’t provide a pressure or a vector flux). Mmg is expecting a sol file that contains, either a metric (for adaptation mode), or a level-set distance (for isosurface discretization mode), or a displacement field (for lagrangian movment mode).

Best Regards,
Algiane

[mrbenson75]

Thanks for your complete explanations, that’s helped me a lot !

• To compile (with Visual studio) mshmet i need to modify as follow :

static int gauss(int n,double[6]|6] m,double *x,double *b,char dbg)

I don’t know why the compiler doesn’t accept double[n][n].

• Which version of mshmet do you use ? I downloaded mshmet from the branch olderVersionThatWorks in the official mmg github. It seems to be quite old :

– MSHMET, Release 2.3c (Aug. 25, 2009)
Copyright (c) LJLL, 2007-09
…
– PHASE 2 : METRIC
Warning: laplace not implemented in 3D. (is that normal ?)

When using your same parameter values in isotropic mode, i don’t have the same metric field

Best regards.

[Algiane]

Hi,

Sorry for the confusion, I totally forget that I had older version of mshmet on my laptop and the binary I was using was not the expected one.

So:

• I think that MSVC does not allow to allocate on the heap an array by specifying a size which is not known at compile time, it is (probably) why the double[n][n] don’t work;
• to my knowledge there were no recent devlopments within mshmet, except its refactoring to allow to use it in library mode (but there is no 3D in this relatively recent version);
• I have fixed few things in the OlderVersionThatWorks branch:
  • an error in the computation of the hessian;
  • a comparison to epsilon at simple precision that was too large;
  • the default normalisation of the hessian values (they were not normalized, now they are normalized by the infinite norm of the solution). The new default value is consistent with what is done in master branch;

Normally you should have the same results as me now… I cross my fingers!

Regards,
A.

[mrbenson75]

Hi @Algiane
Thanks for you answer, i get the right refinement now when compiling with the corrected mshmet and the right version of mmg3d ! Both iso and aniso modes take a bunch of time. Aniso mode gives some warnings :

Warning: MMG5_lenEdg: at least 1 negative edge length (-5.011612e-004)
Warning: MMG5_interpreg_ani: at least 1 impossible metric interpolation.
Unable to complete surface mesh. Exit program.

Maybe my initial mesh is too coarse

Thanks.

[Algiane]

Hi,

• Indeed, Mmg is pretty slow on this test case. Normally I advise users to install scotch and enable its use within Mmg but this tool is not available under MSVC (scotch renumber the mesh elements during adaptation to reduce cache misses). I think that the remeshing time will be smaller for the other iterations (if you are within an iterative process) because your mesh will be closer from the target mesh (here, Mmg has lot of works to do).

• the warnings in anisotropic mode are not normal but happen very often (even more in the presence of non-manifold edges and sharp edges). We are currently trying to robustify and solve some of these issues. Most of time, they can be quietly ignored (it can be a good thing to check visually the surface mesh). Though, the last sentence is more annoying (Unable to complete surface mesh. Exit program.) it is expected to be printed only after an error (not a warning). Is it possible to copy the entire terminal output?

Thanks by advance,
Algiane