Hi there!
I am using parmmg3d inside FreeFem and want to to the following:
I build a mesh, compute the current mesh size (per DOF), distribute it, solve an eigenvalue problem on it. Then with the found eigenfunction and eigenvalue I estimate the error eta on each element. For each DOF sitting on an element with eta > alpha * maxeta, the mesh size is halved and I want the mesh to be remeshed according to this new desired mesh size.
In FreeFem in 2D this works fine using adaptmesh. In 3D using parmmg3d it also does something that looks approximately right, but I would like to understand what exactly it does.
Especially, I have no idea what mshmet does. I tried to do the above without it, but then much too much is refined.
If someone could throw some light for me on what is happening or where I can read about it I’d very much appreciate it.
Thanks!
Hi,
ParMmg is a (recent) research software so it may not always produce the expected results. I think that the first thing to do is to understand if the issue is in the metric computation or in the mesh adaptation with respect to this metric.
I have few questions :
- are you using an isotropic or anisotropic metric?
- if you try to adapt your mesh using Mmg (serial mesh adaptation) instead of ParMmg, did you get statistically the same results than with ParMmg (if serial adaptation is possible of course)?
- if you increase the verbosity of ParMmg to 5, what is the output of the edge length histogram?
- what gives the vizualization of your input metrics (the mshmet one and yours)?
- are you able to get the wanted mesh if you provide a constant metric on the whole mesh?
Thank you by advance,
Best Regards,
Algiane
Hi Algiane,
Thanks for your answer. I’ll try to reply your questions but I am very new to Mmg and quite frankly a bit overwhelmed  So I’m not sure my answers actually answer your questions…
So I’m not sure my answers actually answer your questions…
- I intend using isotropic metric but I don’t know how to pass this to the program. I tried putting iso=1 but then it did not refine at all, the number of elements stayed the same.
- Using Mmg, from an original mesh with 264 vertices and 720 tetrahedra after one adaptation the output of Mmg says 27,682 vertices and 147,386 terahedra.
Using ParMmg with 2 processes, from the same original mesh after one adaptation the output from ParMmg says 45,542 vertices and 245,225 tetrahedra. - The edge length histogram for when I put in my mesh size directly is:
HISTOGRAMM:
0.30 < L < 0.60 1020 0.34 %
0.60 < L < 0.71 9635 3.20 %
0.71 < L < 0.90 82105 27.25 %
0.90 < L < 1.30 192612 63.92 %
1.30 < L < 1.41 13237 4.39 %
1.41 < L < 2.00 2716 0.90 %
and when I put my mesh size into mshmet and use that as metric:
HISTOGRAMM:
0.00 < L < 0.30 2374 9.04 %
0.30 < L < 0.60 14830 56.47 %
0.60 < L < 0.71 3063 11.66 %
0.71 < L < 0.90 3556 13.54 %
0.90 < L < 1.30 2382 9.07 %
1.30 < L < 1.41 53 0.20 %
1.41 < L < 2.00 5 0.02 %
- Sorry I don’t understand this question. But when I look at the mesh size and the resulting metric from mshmet, it seems to me that mshmet increases the values somehow and even entries in the array that were the same are not the same anymore.
- When I put in a constant metric, the mesh is refined uniformly - which is what I expect.
Thank you very much for your help!
Hi,
Ok, so, from what you are saying:
-
Setting the
isoparameter to 1 should be the suitable way to ask for isotropic adaptation; The other main arguments of mshmet are: (i) the solution field for which you want to control the error of interpolation, (ii) the maximal threshold for the error of interpolation (eps), (iii) minimal (resp. maximal) bounds for edge lengths (hmin/hmax). I often advise to first fit theeps,hminandhmaxparameters in the isotropic case before trying to perform the same adaptation in anisotropic mode (which , I think, is the default mode if you don’t provide theisoargument). -
Mmg and ParMmg don’t produces the same mesh from the same mesh + metric. It can worth to look at the appearance of the generated meshes (by Mmg and by ParMmg). Very probably ParMmg fail to converge and to adapt the mesh everywhere. Maybe you can try to increase the number of iterations of ParMmg (something like 6 iterations for example). Do not hesitate to attach or to link the input mesh and metric and/or the Mmg and ParMmg output meshes (it can help me to identify the problem);
-
Both edge lengths histograms shows that you are imposing entirely different metrics. For the first histo, your mesh seems to have globally the right size of edges (edges between 0.7 and 1.4). The second metric says that edges are too small. A quick remark: when you call mshmet, you don’t impose directly a mesh size, you ask mshmet to compute it for you (it is probably just a matter of wording but as it can hide an misunderstanding of the software behaviour, I prefer to specify this).
Do not hesitate to attach picture or data  if possible, I will try to give a look.
if possible, I will try to give a look.
Best
Hi Aligane,
Thanks for your answer and sorry for only getting back to you now.
This is what I thought, but what if I want to pass a particular mesh size to parmmg3d? This is why I pass my mesh size vector directly to parmmg3d instead of generating a metric with mshmet.
And what does mmg3d/parmmg3d do with the given metric?
This is an example of what I did in 2D using FreeFem function adaptmesh.
You can see the error is largest on the triangles around the boundary, so I mark them and half the mesh size on the corresponding DOFs. In the next adaptation step you can see that the triangles are smaller around the boundary and the same elsewhere, as required.
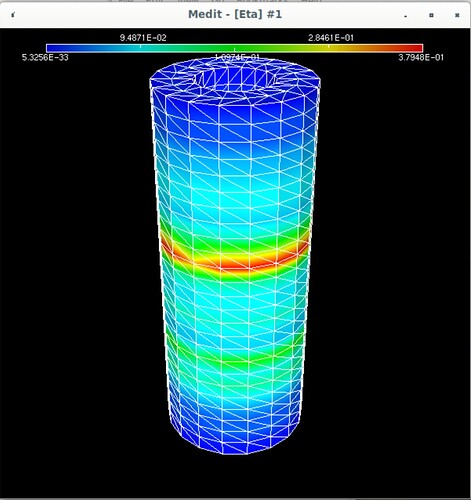
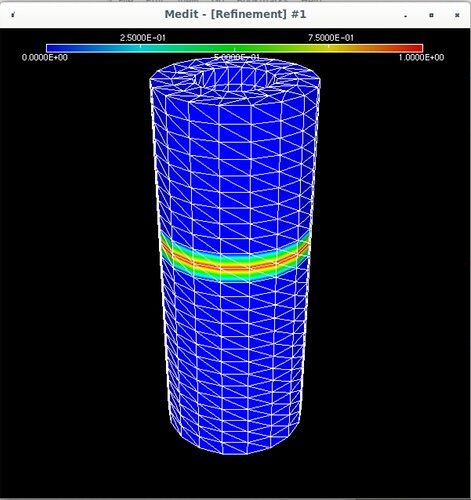
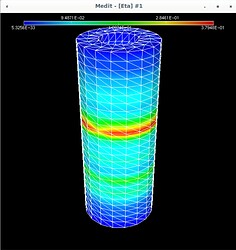
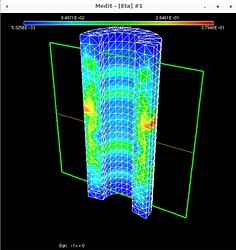
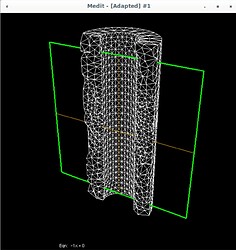
Now in the 3D case I need to do the same. I’ve attached some pictures to show what is happening.
Using Mmg, the following pictures show first the error estimate, then the correct marking and then the refined mesh where I put the mesh size directly as metric (without mshmet). On the whole, it looks correct, as the mesh was (more) refined where the initial mesh was marked, but why was it also refined in the other places?
The mesh size I pass to mmg3d is an array with numbers around 0.25 which makes sense, because the radii of the pipe are 0.5 and 1.0 (so the annulus has width 0.5) and the mesh size initially is about half of the annulus width (except the places where I want to refine have halved values, around 0.12).
And I have a question regarding this histogram coming out of mmg3d: it claims that the average length is 1.35 and smallest length 0.59 but this obviously is not true, looking at the last picture above. Clearly, given the geometry, there are edges of size around 0.2 and smaller. So what does this data mean?
RESULTING EDGE LENGTHS 11934
AVERAGE LENGTH 1.3576
SMALLEST EDGE LENGTH 0.5909 1890 1962
LARGEST EDGE LENGTH 3.1306 501 574
0.71 < L < 1.41 7092 59.43 %
HISTOGRAMM:
0.30 < L < 0.60 18 0.15 %
0.60 < L < 0.71 774 6.49 %
0.71 < L < 0.90 2034 17.04 %
0.90 < L < 1.30 3564 29.86 %
1.30 < L < 1.41 1494 12.52 %
1.41 < L < 2.00 2394 20.06 %
2.00 < L < 5.00 1656 13.88 %
Thank you so much for your efforts to help!
Hi,
Regarding the size of your input mesh, I think that you will not be able to have suitable results with ParMmg: the algorithm is based on iterative remeshing-repartitionning with freezed interfaces between partitions. With this kind of algo, too small partitions constrain the remesher too much. I think that you should try to have suitable results with Mmg serial adaptation first.
The printed edge length histogram prints the statistics of lengths computed in the input metric space. It means that we always target unitary lengths: lets guess that you provide a constant input size map of size 0.25, let \mathbf{e} be an edge that will have a euclidean length of 0.25, it will have a length of 1 in your metric space.
The length in the metric is computed as following: \|\mathbf{e}\| = \sqrt{ <\mathbf{e},\mathbf{e}>_{\mathcal{M}} } = \sqrt{\mathbf{e}^T \mathcal{M}\mathbf{e}}.
In practice:
- it is not possible to have edges of exactly size 1 so Mmg tries to have edges between 0.6 and 1.3.
- your intput size map is modified by Mmg:
- along the surface, it is intersected with the size map coming from the hausdorff parameter;
- sizes are smoothed to satisfy the gradation parameter (to ensure good qualities, the jump between the metric values at 2 nodes connected by an edge should not be too large).
You can read the following paper to have some info on metrics and gradation:
Mesh gradation control, H. Borouchaki and F. Hecht and P.J. Frey, Int. j. numer. methods engng., 43, 6, 1143-1165, 1998.
The input edge length histo printed by Mmg/ParMmg computes lengths in your input metric while output edge length histogram computes lengths in the modified metric. As far as I can see, ParMmg fails to adapt your mesh: having only 60% of edges in the target is too few (in serial we hope to be around or above 90%).
For the fact that your mesh is refined in other places than expected, I seems very likely due to the gradation. Maybe you can try to run (with Mmg) and with a disabled gradation (hgrad -1).
Best Regards,
Algiane
Hi Algiane,
Thanks again for your reply, this is very helpful.
As for the size of the mesh, I’m sorry I failed to mention this; the output in the last and this post are from Mmg. I’m looking to use ParMmg on a larger mesh, what I’m doing right now is just to see what is happening on a simplified model.
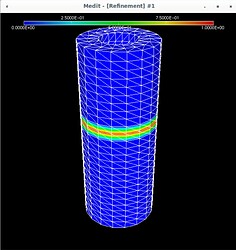
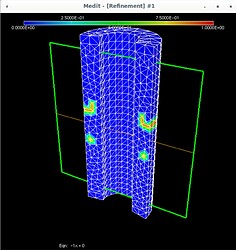
Setting hgrad -1 I’m quite happy with the result:
Initial mesh
Error indicator
Marking for refinement
Refined mesh
And the histogram output after remeshing is:
-- RESULTING EDGE LENGTHS 38204
AVERAGE LENGTH 0.9865
SMALLEST EDGE LENGTH 0.4090 3322 3109
LARGEST EDGE LENGTH 1.9855 1068 1292
0.71 < L < 1.41 34346 89.90 %
HISTOGRAMM:
0.30 < L < 0.60 918 2.40 %
0.60 < L < 0.71 2365 6.19 %
0.71 < L < 0.90 10908 28.55 %
0.90 < L < 1.30 21164 55.40 %
1.30 < L < 1.41 2274 5.95 %
1.41 < L < 2.00 575 1.51 %
which, if I understood correctly, is good?
Further I notice that when I remesh again, the percentage of edges within (0.71;1.41) increases.
Hi,
Thanks for this feedback.
It is better yes!
Mmg uses an iterative algorithm whose convergency is checked by comparing the number of operations of each type (split, collapses, etc.) performed. When you call Mmg on its resulting mesh, most of time it will perform few iterations and improve the edge length histogram.
Best Regards,
Hi I need the same thing for my code. I need to make mesh which has h=0.247 on a unit cube. How can I build this mesh?