Level set mesh adaptation

User Help
#1

Hello,
i want to thank you firstly for this forum.
I have a question concerning the mesh adaptation using mmg3D.
let say that i have a mesh file and i want want to adapt it inside a sphere, the first step to do is to create an implicit sphere and produce a .sol file in order to pass it finally to mmg3D,

But i want a real example about this procedure to follow please on any 3D mesh file to adapt it inside a sphere and thank you.

#2

Dear abba,
thank you for your message.
I am not quite sure I understood what you are aiming at: is it that you want to create a new mesh which contains a mesh of the sphere as a submesh (by providing the information about the sphere by means of a level set function)? Or do you want to simply refine the mesh around the sphere ?
Thank you again for your interest,
best,
Charles

#3

Hello,
i want to start with a simple 3D mesh (a face
for example), and to adapt it to a sphere that contains it, so as a
result we will have a sphere that contains our initial mesh with an
adaptive triangulation. like the plane in this image

Course-logo-web.jpg2200×1600 1.77 MB

Thank you,

#4

Hello,

Sorry for the delay.

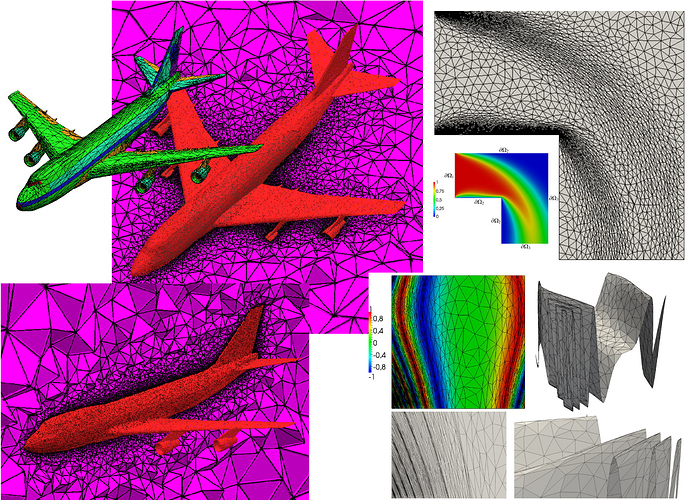
If I understand well, you want to use a level-set function to define your initial 3D face mesh inside the mesh sphere and then be able to discretize the surface mesh (ie the 3D face mesh) inside the sphere mesh.

Here are the steps to follow:

  • compute the signed distance function that represent your surface mesh inside the sphere mesh (for each node of the sphere mesh, you must compute the minimal euclidean distance between the node and your surface mesh).
    This function must be 0 at the surface mesh, negative inside and positive outside.
    Save the discrete signed distance function at the sphere mesh nodes at the medit solution format (if you work with a medit mesh) or as $NodeData inside a gmsh mesh.

  • discretize the implicit function using mmg3d:
    mmg3d_O3 -ls 0 sphere.mesh -nr

The -nr option specify that after the implicit surface discretization, during the mesh optimization, we don’t want to detect sharp angle. The reason is simple: the distance function is a smooth function.

This process will work but I think that you will not recover a good representation of your aircraft because this geometry is very hard to capture with an implicit function (lot of sharp angles that will be lost during the process, airfoils (which means very thin volumes)… )…

The level-set discretization is more adapted to shape optimization.

I hope this will help,

Best Regards,

Algiane

1 Like