Hello,
I will answer in multiple posts.
For the first post, I will try to answer to the main questions about Mmg.
1. Is “excluding silver tetrahedra” part of Mmg3d features?
Yes
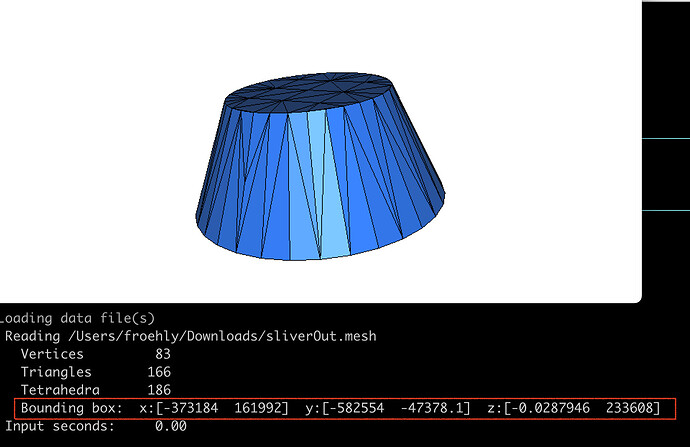
Mmg checks the volume of the input tetrahedra, raises an error message and stops if it detects volumes smaller than 1e-15. Thus, Mmg wil refuse to remesh a mesh containing input slivers.
We don’t want to start from lower volumes because numerical errors while reading/writing the mesh are becoming predominant.
2. Is Mmg checking the validity of the input mesh?
In a nutshell
Only partially
We don’t check the mesh conformity for example. For 3D surface mesh we also don’t check surface intersections…
But, for example, we check and try to fix issues in the provided boundaries of 3D meshes (triangle duplications, missing triangles…).
Why?
-
There are lot of ways for a mesh to be erroneous and we just miss time to add those checks.
Moreover, as we start from an existing mesh, the question/issue may be reported to the mesh generator: does it check the validity of the output mesh it returns?
-
It is why we ask our users to try to provide a valid finite element mesh as input (but I know that it may be tricky to check).
With a valid FE mesh, Mmg3D will return a valid FE mesh too or warn you and return an error value if it is not sure that the mesh is still a valid FE mesh (the main possible error inside Mmg is to end with a non-conforming mesh).
What happens if I start from a non-valid FE mesh?
The Mmg behaviour will be undefined:
- in most of cases, the mesh will be successfully remeshed but you will end-up with a non-valid FE mesh of the same type or your input;
- the code may fail during analysis;
- the code may fail during the remeshing;
- cases where the code livelock are pretty rare but may happen.
3. Why not set an absolute value for the hausdorff parameter?
Asking for an absolute value for the Hausdorff (I mean a value that doesn’t depend on the object size) has been tried but didn’t produce good results.
I am not sure if there were some numerical issues (It has been tried before I arrived on the project) but regarding the usability, I think that even with an absolute parameter, it is often necessary to manually change the default value (I will explain why after) and it is less intuitive to play with an absolute parameter than a relative one (the sensitivity of the absolute parameter is related to the object size and curvature due to the normalization…).
4. Why it is not possible for Mmg to set a suitable default value for the Hausdorff?
The hausdorff value you want to use depends:
- on the size(s) of the object(s) you have inside your mesh;
- on their curvatures (you will have no issue with the haudorff on cube meshes, whatever its value);
- on the precision the user wants to approximate its boundaries.
It is just impossible to have a suitable value in some cases : for example, in fluid mechanics, there is often a very small object (let’s say an airplane), in a large bounding box (a sphere). In this case you want 2 hausdorff totally different on both surfaces because the hausdorff suitable for the bounding-box will lead to have almost no elements to represent the airplane, and the hausdorff suitable for the airplane will lead to refine a lot on the sphere surface.
5. Does Mmg guarantee to improve my mesh?
In a nutshell
No
“Improving” a mesh is a term that needs to be defined. The main aim of Mmg is not to improve the mesh quality but to produce an output mesh closer to the user’s needs than the input mesh. Of course, the element quality plays a role and we hope to have a sufficient minimal quality in our output mesh but we don’t try to “improve” the mesh quality.
In practice, what you need to run a computation on your mesh is a “not too bad” worst element (and the notion of “not too bad” depends on the numerical solver you use).
A very simple example that I like is provided in the following picture: the left mesh is “perfect” in term of quality (all elements are equilaterals) but it cannot be used in most FE solvers because one of the elements contains 2 boundary conditions. Mmg will produce the mesh on the right, which has a lower quality but can be used by all FE solvers: the quality is sufficient enough and all mesh elements have only one BC.
More details about the remeshing process
- The mesh adaptation process is an overconstrained problem: we try to have equilateral elements (in a metric space), to have a suitable boundary approximation (even in very curved area) that respect the geometric features and the topology, with a “minimal” number of elements and, in some case while respecting an input size map. To do that, every remesher make compromises and choose to favorize some of the previous criteria comparing to the others.
- The mesh adaptation process is also very heuristic: we interleave steps and operators (splits, collapses, swaps) hoping that it will produce a good result on a majority of the configurations. Each operator destroys the work of others (splits and collapses help to have suitable edge lengths but gives bad quality elements, swaps improve the quality but break the edge length…). It is the succession of operators that allow to obtain a mesh closer from the user prerequisite… but predicting that it will actually work before applying the entire sequence of operators is not so easy.
- Near boundaries, the respect of surface geometry and of the topology are huge constraints for the remesher and the generic local operations implemented may simply be inapplicable (because improving the mesh asks to pass by a step with negative volumes or with non local operators).
The algo implemented inside mmg is the result of the experience and work of researchers and we hope that it will give good results in most of cases ( ).
).
But, depending on the test case, you may have better result with one remesher than another one, it doesn’t mean that one tool is better than the other, just that on the input configuration you provide, an algorithm behaves better than another.
In Mmg:
- we give priority to the boundary approximation (because we start from an input discretization, if we lose boundary infos, we are not able to retrieve them). To have a suitable boundary mesh, we authorize to degrade the tetrahedra… and we have no warranty that we will be able to retrieve the input quality or to improve it;
- we choose to produce a Finite Element mesh: by default we don’t authorize to keep boundary elements with more than one boundary face and, if possible, we split internal edges connecting boundary points (it has a consequence on the mesh quality too);
- we authorize to degrade tetrahedra qualities because we have observed that it helps to unblock some bad situations. We hope to retrieve a better quality at the end but, again, we cannot ensure it.
I hope that it answers to the main questions about what can and can’t do Mmg. Do not hesitate to point me things that I may have missed.


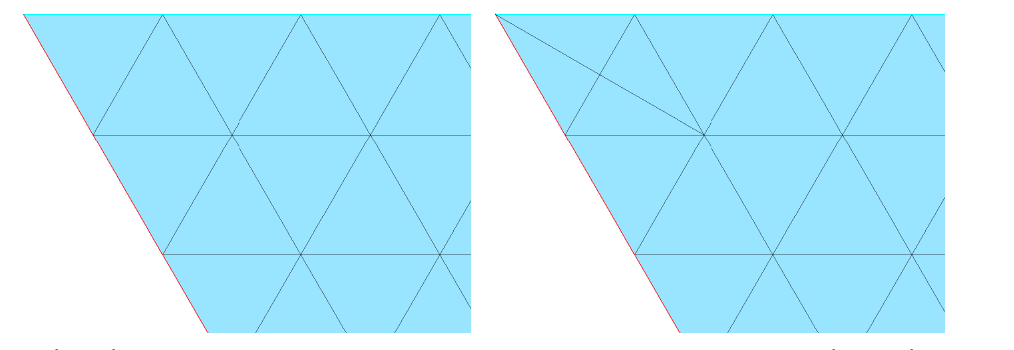
 ).
).