How to set the tensor metric in this heat conductino problem

User Help
#1

Screenshot_20191022_200543
Screenshot_20191022_200543.png1115×994 85.5 KB

Dear sir:
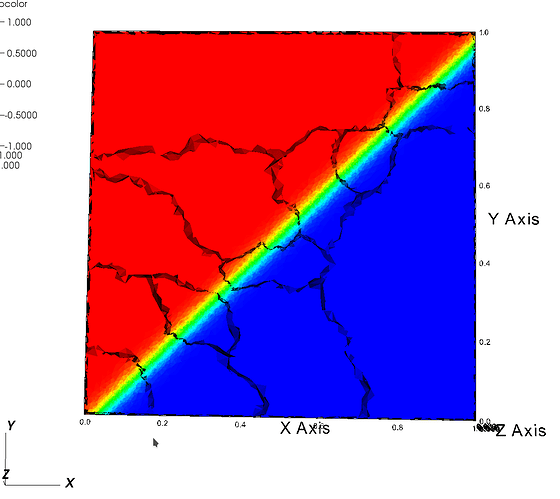
I am solving this 3D heat conduction problem with FVM where large gradient only exist in the diagonal region and the variation of temperature field in the z direction is very small.
The dimension of the box is “1X1X0.04”. Could you please give me some suggestions about how to set the metric tensor:
m11,m12,m13,m22,m23,m33.
I want to set the m11 and m22 with a little value and m33 a relatively large value.
but how to set the m12 and m13.
Regards

#2

Hello,

I suppose that you want to prescribe:

  • the size h1 = 0.02 in the direction x1 = (sqrt(2)/2,-sqrt(2)/2,0)
  • the size h2 = 0.04 in the direction x2 = (sqrt(2)/2, sqrt(2)/2,0)
  • the size h3 = 0.1 in the direction x3 = (0, 0, 1)

Note that (x1,x2,x3) must form an orthonormal basis.

In this case, you can build:

  • a diagonal matrix D such as the diagonal term d_{ii} = 1/(h_i * h_i).
    So:
    • d11 = 2500;
    • d22 = 625;
    • d33 = 100;
  • the matrix of the tensor directions P = (x1,x2,x3)

Finally, you can compute M = inverse( P ) * D * P an give the terms (m11,m12,m13,m22,m23,m33) = (1562.5,937.5,0,1562.5,0,100) to Mmg.

I hope that it will help.

Regards,
Algiane

#3

Thanks.

  1. What is the meaning of “inverse§”, does it mean we obtain the inverse matrix of D?
  2. what is the relation ship between the “direction” and the “Tetrahdraon cell”
    Regards
#4

Hi,

  1. I have edited the previous post (markdown has interpreted the ‘P’ between parenthesis as the paragraph symbol) : you need to compute the inverse of the change of basis matrix P.

  2. On your input mesh there is no relation between the tetrahedra shapes and the directions of your metric:

    • you choose the directions depending on your needs;
    • In the example I give, I have taken directions suitable with the image that you have attached;
    • Most of times, the tensor metric is automatically computed (e.g. using an a posteriori error estimator);
    • The tetra of your output mesh will be oriented in the directions prescribed by the metric.

Regards,

PS : I am a miss, not a sir :wink:

#5

Dear;
I still be confused about the diretions. In the above picture, I want to refine the mesh in the diagonal direction from lower left to upper right. that is in the (1,1,0) direction.
How to obtain these three orthogonal vectors. P1,p2,p3.
Regards

#6

Hi,

The diagonal direction can be given by the vector (1,1,0) but also by the vector (\sqrt(2)/2,\sqrt(2)/2,0) = \alpha (1,1,0) with \alpha = \sqrt(2)/2 (both vectors represent the same direction).

To compute the direction that I give you, I simply apply a rotation of \Pi /2 to the canonical basis (along z) so I end with a vector along the diagonal direction.

Regards,
Algiane