A simple Python code to demonstrate the mesh adaptation using mmg executables

Share Your Meshes
#1

Hello,

Here is a straightforward code (written in Python 3.9 and numpy library) to demonstrate the process of mesh adaptation using mmg executable:

'''
Program to demonstrate the following features of mmg executable:
  1. The mesh file format
  2. A simple mesh generation using mmg2d
  3. The metric file format
  4. A simple metric calculation algorithm
  5. Multi-stage mesh adaptation process

Note: In a real simulation, all the interactions with mmg will be through 
      API calls and not using executables.
 
Useful references & links:
  1. https://pages.saclay.inria.fr/frederic.alauzet/proceedings/Frey_Anisotropic%20mesh%20adaptation%20in%203D%20Application%20to%20CFD%20simulations.pdf
  2. https://www.mmgtools.org/mmg-remesher-try-mmg/mmg-remesher-tutorials/anisotropic-metric-prescription
  3. https://www.mmgtools.org/mmg-remesher-try-mmg/mmg-remesher-tutorials/mmg-remesher-mmg2d/mesh-generation
  4. https://theses.hal.science/tel-01284113

Author: 
  Sourabh Bhat <sourabh.bhat@inria.fr>
'''

import numpy as np
from numpy import sin, arctan
import subprocess


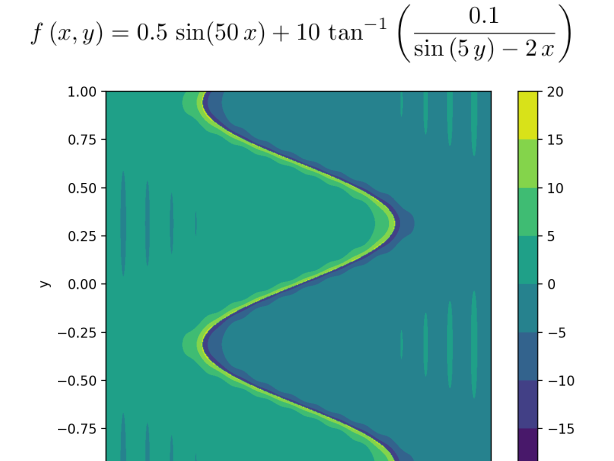
def f(x, y):
    # solution function
    # change this function as needed
    return 0.5 * sin(50*x) + 10 * arctan(0.1 / (sin(5*y) - 2*x))


def hessian_matrix(x, y):
    # Note: In a real application, the Hessian needs to be
    #       computed numerically using solution at the nodes.
    # Here, partial derivatives are approximated numerically (of a known function) for convenience.

    # replace with analytical functions, if necessary.
    dx = 1e-6
    dy = 1e-6
    d2f_dx2 = (f(x+dx, y) - 2*f(x, y) + f(x-dx, y)) / (dx*dx)
    d2f_dy2 = (f(x, y+dy) - 2*f(x, y) + f(x, y-dy)) / (dy*dy)
    d2f_dxdy = (f(x+dx, y+dy) - f(x+dx, y-dy) -
                f(x-dx, y+dy) + f(x-dx, y-dy)) / (4*dx*dy)

    return np.array([[d2f_dx2, d2f_dxdy],
                     [d2f_dxdy, d2f_dy2]])


# main function
def main():
    # Note: In a real simulation, all the interactions with mmg will be through
    #       api calls and not using executables.
    meshfile_path = generate_starting_mesh()

    # Note: The following mesh adaptations can be done in a loop :)

    # first adaptation
    adapt_mesh_using_mmg(meshfile_path)

    # second adaptation (with metric computed on adapted mesh)
    meshfile_path = meshfile_path.replace(".mesh", ".o.mesh")
    adapt_mesh_using_mmg(meshfile_path)

    # third adaptation (with metric computed on adapted mesh)
    meshfile_path = meshfile_path.replace(".mesh", ".o.mesh")
    adapt_mesh_using_mmg(meshfile_path)

    # fourth adaptation (with metric computed on adapted mesh)
    meshfile_path = meshfile_path.replace(".mesh", ".o.mesh")
    adapt_mesh_using_mmg(meshfile_path)


mmg_exe = "mmg2d_O3"


def adapt_mesh_using_mmg(meshfile):
    # Steps:
    #   1. Write metric to .sol file.
    #   2. Call mmg for mesh adaptation.

    # Note: In a real application,
    #       no need to read vertices of current mesh (as they are aready known).
    #       these are the nodes where current solution and Hessians/metric are available.
    # Step 0: read mesh vertices from current mesh
    nodes = read_mesh_nodes(meshfile)

    # Step 1: compute and write metric to sol file
    solution_file = meshfile.replace(".mesh", ".sol")
    with open(solution_file, "w") as file:
        file.write("MeshVersionFormatted 2" + "\n")
        file.write("Dimension 2" + "\n")
        file.write("SolAtVertices" + "\n")
        file.write(f"{len(nodes)}" + "\n")
        file.write(f"1 3" + "\n")
        for (x, y) in nodes:
            m = metric(x, y)
            file.write(f"{m[0,0]} {m[0,1]} {m[1,1]}" + "\n")
        file.write("End" + "\n")

    # Step 2: Call mmg for mesh adaptation
    subprocess.call([mmg_exe,
                    '-in', meshfile,
                     '-sol', solution_file])


def metric(x, y):
    # A simple definition of metric, for demonstration purposes only!
    # In a real appliation, you also need to
    #      modify the metric based on edge-size constraints, aspect ratio limit, number of elements etc.
    hessian = hessian_matrix(x, y)
    # make positive definite
    evals, evecs = np.linalg.eig(hessian)
    abs_evals = np.clip(np.abs(evals), 1e-8, 1e+8)
    return evecs * abs_evals @ np.linalg.inv(evecs)


def generate_starting_mesh():
    # Note: you can use other software for mesh generation (such as gmsh)
    # Here, we are using mmg for mesh generation to keep it simple (and stupid!).

    input_geometry = "input.mesh"
    vertices = [(-1, -1), (1, -1), (1, 1), (-1, 1)]
    edges = [(1, 2), (2, 3), (3, 4), (4, 1)]  # edge connectivity
    with open(input_geometry, "w") as file:
        file.write("MeshVersionFormatted 2" + "\n")
        file.write("Dimension 2" + "\n")
        file.write("Vertices" + "\n")
        file.write(f"{len(vertices)}" + "\n")
        for (x, y) in vertices:
            file.write(f"{x:10.5f} {y:10.5f} {0:5d}" + "\n")

        file.write("Edges" + "\n")
        file.write(f"{len(edges)}" + "\n")
        # use as per your boundary tags. Here using arbitrary tag number 7
        edge_tag = 7
        for (start, end) in edges:
            file.write(f"{start} {end} {edge_tag}" + "\n")
        file.write("End" + "\n")

    starting_mesh = "output.mesh"
    # call mmg to generate initial mesh
    subprocess.call([mmg_exe,
                    '-hmax', '0.2',
                     '-in', input_geometry,
                     '-out', starting_mesh])
    return starting_mesh


def read_mesh_nodes(meshfile):
    nodes = []
    with open(meshfile) as file:
        for line in file:
            if line.strip() == "Vertices":
                break

        num_nodes = int(file.readline())
        for i in range(num_nodes):
            x, y, tag = file.readline().split()
            nodes.append((float(x), float(y)))
    return nodes


if __name__ == "__main__":
    main()

This is a self contained program which generates its own mesh and adapts the mesh using mmg2d. You will need to get mmg from http://www.mmgtools.org/mmg-remesher-downloads or compile it from source to obtain the executable mmg2d_O3. To visualize the generated / adapted mesh you can use Medit (https://github.com/ISCDtoolbox/Medit).

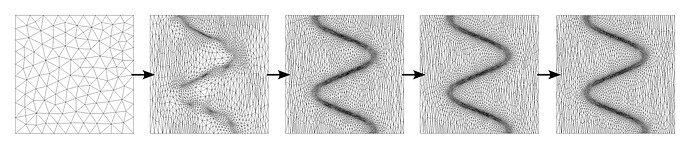
Here is an example function which is used for mesh adaptation:
function_1

which produces following series of adaptations:

evolution_of_meshes
evolution_of_meshes1920×414 166 KB

Other references which may be useful:

  1. https://www.mmgtools.org/mmg-remesher-try-mmg/mmg-remesher-tutorials/anisotropic-metric-prescription
  2. https://pages.saclay.inria.fr/frederic.alauzet/proceedings/Frey_Anisotropic%20mesh%20adaptation%20in%203D%20Application%20to%20CFD%20simulations.pdf
  3. https://www.mmgtools.org/mmg-remesher-try-mmg/mmg-remesher-tutorials/mmg-remesher-mmg2d/mesh-generation
  4. https://theses.hal.science/tel-01284113

Notes:

  1. In practical applications, the use of shared library is a preferred way to interact with MMG using API calls. However, this example code will be useful in understanding the algorithm for mesh adaptation.
  2. In a real application you will have other constraints and requirements for metric calculation, such as element size limits, aspect ratio limits, number of elements etc. Here, a very simple definition of metric is used.
  3. A few more comments are written in the code at appropriate places.

Cheers!
Sourabh Bhat
CARDAMOM Team, Inria

1 Like