Dear all,
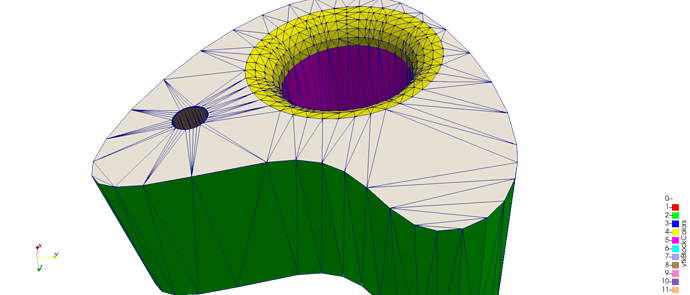
I’d like to use mmgs to build a surface mesh to use for computations from an stl-like triangulation that looks like this.
(I think my problem is quite similar to the Mesh decimation example on the website)
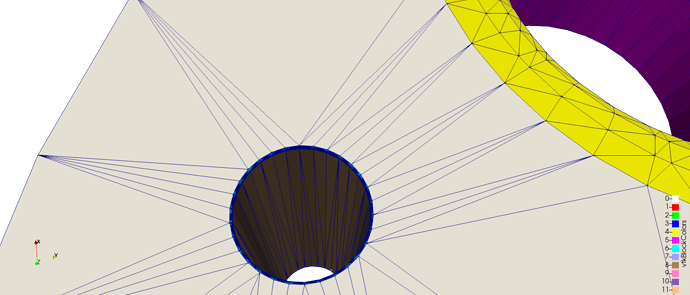
For this, I prescribe an isotropic metric which, at any point is the length of the smallest edge containing this point. This mostly works well (if I re-project on the CAD model after at least), except in areas like the cylindrical hole in the second image. Indeed, the mesh is much too fine in the while cylinder, it is not only refined in the fillets.
I was thinking about splitting all the triangles in the stl-like triangulation before calling mmsg to avoir having long edges with small cells at both sides. Is is possible with mmg or should I do it by hand? Is there a better solution, how did you proceed for your example?
Thank you
Xavier